Unterlagen zum 3. Kurstag

Fernrohroptiktheorie

Grundlagen

• Das Objektiv sammelt und konzentriert das Licht eines Sterns: Lichtsammelwirkung
• Mit Okular wird das Fernrohr zum "Lichttrichter": Vorne kommt ein großes Bündel hinein, hinten kommt ein dünner Strahl heraus, den das Auge ganz aufnehmen kann.

• Das Fernrohr lässt ferne Objekte größer erscheinen: Vergrößerungswirkung
• Das Motiv erscheint am Himmel unter einem sehr kleinen Winkel. Das Objektiv erzeugt ein Bild des Motivs, welches mit der Okular-lupe vergrößert betrachtet wird.

Kenngrößen des Fernrohrobjektivs

• Durchmesser: D in mm => bestimmt die Lichtmenge die vorne reinkommt. Der Durchmesser wird oftmals auch in Zoll angegeben (1Zoll = 25.4mm)
• Brennweite: f in mm => bestimmt den Bildmassstab des erzeugten Bildes
  Beispiel: f = 1000mm: Bild von Sonne / Mond ca 9mm groß
• Das Verhältnis aus Durchmesser und Brennweite wird als Öffnungsverhältnis bezeichnet, der Kehrwert daraus als Öffnungszahl N.
  N = f / D. Die Öffnungszahl entspricht dem Blendenwert aus der Fotografie

Okulare, der wechselbare Teil des Fernrohrs

• Okulare wirken wie Lupen, durch die das vom Objektiv erzeugte Bild betrachtet wird.
• Okulare haben eine Brennweite fOk, das ist ihre wesentliche Kennzahl
• Kleine Brennweite => hohe Vergrößerungswirkung
• Die momentane Vergrößerung des Fernrohrs ergibt sich immer aus der Kombination Objektiv & Okular:
  Berechnungsformel: V = f / fOk
• Der Durchmesser des hinten aus dem Okular austretenden Lichtbündels ist die sog. Austrittspupille, eine wichtige Größe zur Auswahl der sinnvollen Okularbrennweiten. Das Auge setzt hier obere und untere Grenzen.
• AP = D / V
• AP = fOk / N

Wahres und scheinbares Gesichtsfeld

• Das Objektiv erzeugt ein reales Bild in der Brennebene. Die Objektivbrennweite bestimmt den Maßstab dieses Bildes.
• Okulare haben eine physikalische Feldblende. Diese bestimmt den sichtbaren Ausschnitt aus dem vom Objektiv erzeugten Bild. Dieser Ausschnitt ist dann das "wahre Gesichtsfeld" dieser Kombination von Objektiv und Okular am Himmel.
• Das "scheinbare Gesichtsfeld" ist dann der Winkel, unter dem dieser sichtbare Ausschnitt dem Betrachter erscheint. Das SG ist eine wichtige Eigenschaft des Okulars.
  Das SG variiert zwischen 20° und >100°: Blick durch eine lange Papierrolle vs. Blick aus dem Fenster.
• Weitwinkelokulare mit großem scheinbaren Gesichtsfeld sind aufwändiger und teurer als solche mit "Tunnelblick". Bei Planetenbeobachtung zB reicht Tunnelblick aber völlig aus.

Bildbeispiel: Vergrößerung

Zwei Okulare mit gleichem scheinbaren Gesichtsfeld, aber deutlich unterschiedlicher Brennweite:

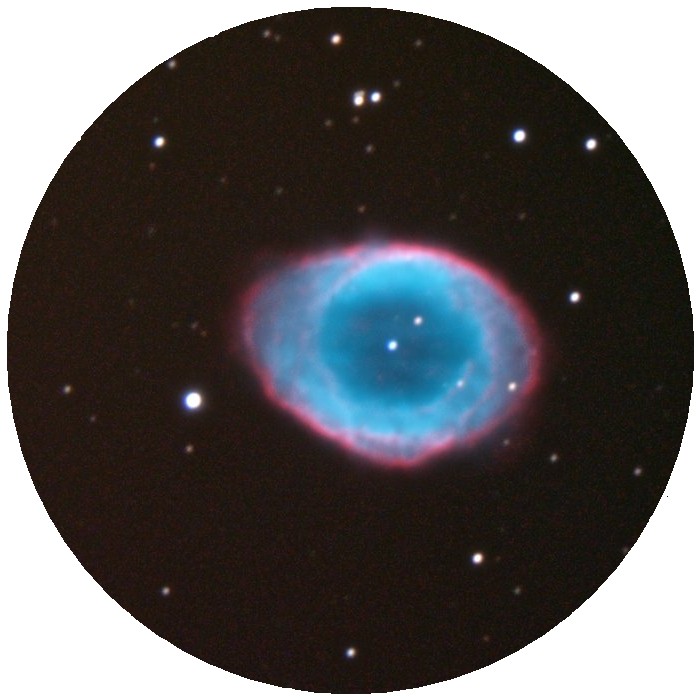Kleine Vergrößerung, größeres wahres Gesichtsfeld

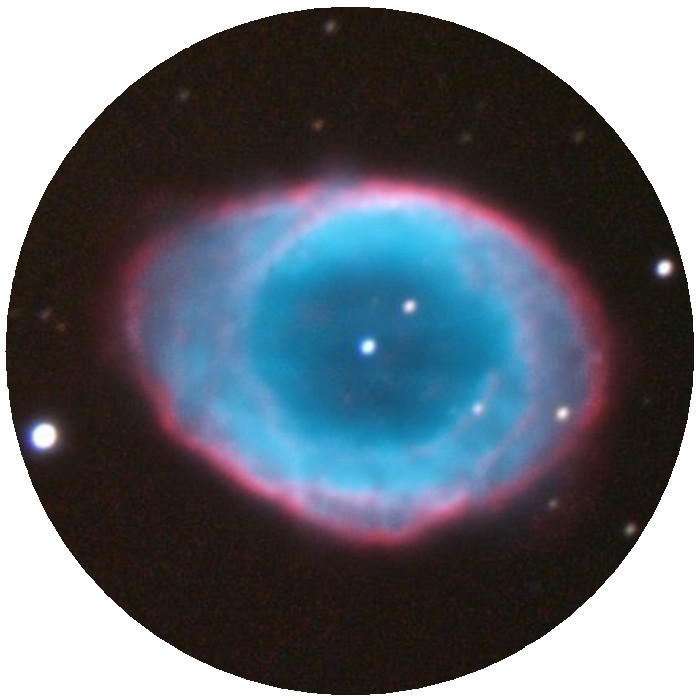Große Vergrößerung, kleines wahres Gesichtsfeld

Bildbeispiel: Scheinbares Gesichtsfeld

Zwei Okulare mit gleicher Brennweite, aber stark verschiedenem scheinbaren Gesichtsfeld

Kleines scheinbares Gesichtsfeld eines "Planeten-okulars"

Großes scheinbares Gesichtsfeld eines Weitwinkel-okulars

Rechenbeispiele

• Objektiv: D = 200mm, f=1200mm, (f/6 oder N=6), ein typischer Einsteigernewton
• Okular: fOk = 40mm, ein 2" WW-Okular mit langer Brennweite zum Aufsuchen der Objekte
• => Vergrößerung V = 1200mm / 40mm = 30x
• => Austrittspupille AP = 200mm / 30x = 6.7mm (= 40mm / 6)

Vergrößerung, sinvolle Grenzen

• Maxmimale Vergrößerung: Vmax = 1.5 * D (in mm), hier also ca 300x
  Faustregel: minimales fOk = N * 2/3
• Minimale Vergrößerung: Vmin = D / 7, hier also 30x => maximale fOk = 40mm
  Ggf aber auch Weitwinkelokular mit dem gleichen Feld und höherer Vergrößerung
  Oder ein "Aufsuchokular" mit eigentlich zu großer AP, aber dem maximalen Feld am Himmel

Okularwahl

Okularwahl ist ein weites Feld, es gibt viele verschiedene Typen in allen Brennweiten und Preisklassen.
Neben technischen Aspekten sind auch persönliche Vorlieben wichtig, nicht jeder kommt mit jedem Okular gut zurecht, auch bei sehr teuren Konstruktionen

Mindestens drei Abstufungen sollten es schon sein:

• Maximales Feld, minimale Vergrößerung (AP = 7 mm)
• Minimale AP, Maximale Vergrößerung für Planeten und Doppelsterne (AP = 0.7 mm)
• Eine weitere, auch eher kurze Brennweite (AP vielleicht 2 mm)