Sky Brightness

Martin Elsässer, 2018

I tried to implement a very simple 2D model of scattered light in our atmosphere after sunset to judge the brightness of the sky through which we would try to see a thin lunar crescent.

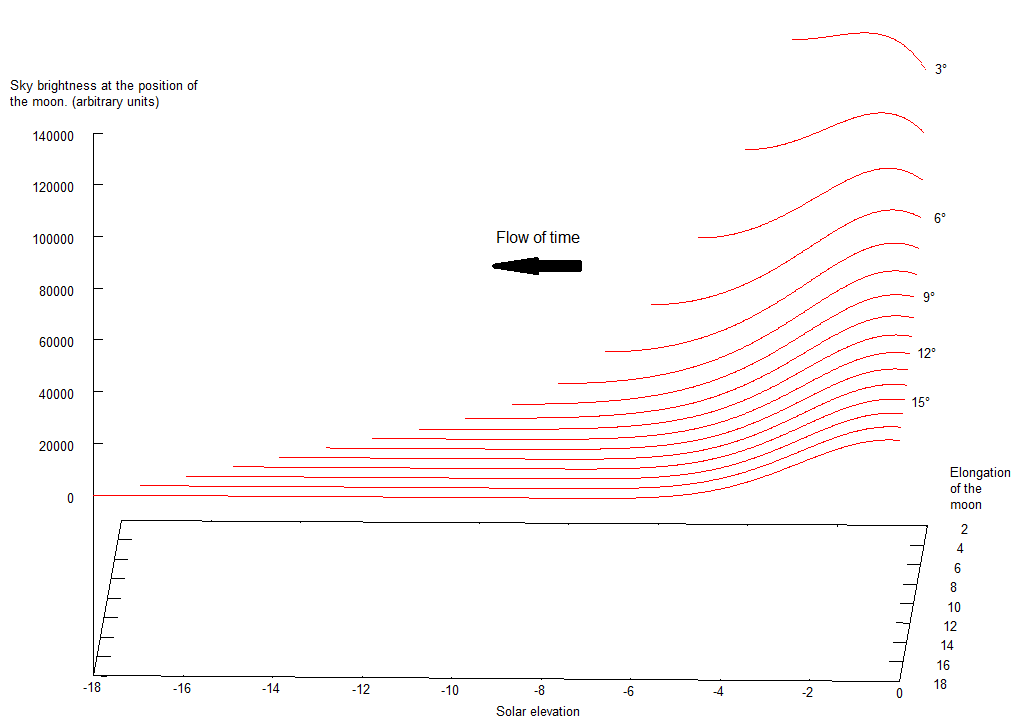
This diagramm shows the brightness of the sky for various values of sun elevation (below the horizon) and lunar elongation.

• X shows the (negative) elevation of the sun, so time moves from right to left.
• Towards the back (lines higher up) the elevation of the moon decreases, from 18° to 3°. The smaller the elongation, the brighter the sky at the position of the moon.
• The altitude of the moon would be the sum of the elongation and the (negative) solar elevation.
• Straight up the brightness of the sky at the position of the moon is shown for various elevations of the sun. The lines stop when the moon sets.

Results

• If elongation is large enough, then the sky brightness near the moon generally drops after sunset.
• The contrast between moon and sky should generally improve over time after sunset.
• There is also a lower limit of solar elevation where no significant further improvement happens. This limit somewhat corresponds to the -6° value of civil twilight.
• The largest improvements happen when the sun drops down to -6° elevation.

Limitations of the underlying model

• The moon is always assumed to be direcly above the sun
• The model of the atmosphere is quite simple, just using the std. barometric density
• The model of scattering is extremely simpel, no directional component, no variation for different wavelengths
• Absorption is ignored
• Light moves straight, refraction is not considered
• The sun is modelled as a dot at infinity
• ...

ToDos

1. Extend the modell to 3D, to get a map of sky brightness above the horizon.
2. Actually measure the change of brightness of the twilight sky on a clear evening/morning.
3. Search for better treatments of this topic in the literature. All of this will have been done before and better, most surely.